Structural Time Series Modelling: Forecasting Air Passenger Numbers

Published Jun 13, 2023 by Michael Grogan

The purpose of this article is to illustrate the use of a Structural Time Series model to forecast air passenger numbers using the Air Traffic Passenger Statistics dataset from DataSF Open Data, which is licensed under the Public Domain and Dedication License (PDDL).

Business Context

The airline industry is very dynamic. As we have seen both pre and post-COVID, passenger demand can change quite quickly.

At the start of the pandemic, passenger numbers collapsed due to travel restrictions. However, the speed at which passenger demand rebounded was equally as surprising.

Forecasting passenger numbers is an important task for an airline — as this will have implications for factors such as what type of aircraft should be deployed on a particular route, estimated fuel costs, expected revenue from a route, among others.

Therefore, an airline that is looking to forecast passenger numbers needs to use a time series model that can quickly react to unanticipated “shocks”. Traditional time series models such as ARIMA are not necessarily the best choice for this.

Data and Modelling

For this problem, it was chosen to analyse historical air passenger data for British Airways — specifically for enplaned passengers travelling internationally to Europe from July 2005 to December 2022.

The time series model will be built using data up until December 2021 — and then the forecasts for 2022 will be compared with that of the actual. Due to a collapse in passenger numbers during the initial stages of the pandemic, data for May 2020 was not included in the dataset. For the purposes of data analysis, it was decided to include a value of 106 passengers for May 2020 — which is the same as that recorded for April 2020.

For this analysis, a structural time series model was fitted to the data using the StructTS function as included in the base package stats in R. Specifically, the structural model for the time series is fitted by maximum likelihood — whereby the goal is to generate a probability distribution that maximises the likelihood of observing the forecasted passenger numbers that are predicted by the model.

The below analysis was conducted with reference to the original analysis of the Nile river data by Petris, G., & Petrone, S. (2011), who authored the State Space Models in R paper for the Journal of Statistical Software under the Creative Commons Attribution License (CC-BY).

Analysis

The structural time series model for air passenger count was generated and plotted as follows:

flights_ts <- ts(mydata$passenger_count[1:198], start = c(2005,7), frequency = 12)
flights_ts

flights_structTS <- StructTS(flights_ts, "level")
flights_structTS

plot(flights_ts, type = "o", ylab='Passenger Numbers', xlab='Year')
lines(fitted(flights_structTS), lty = "dashed", lwd = 2)
lines(tsSmooth(flights_structTS), lty = "dotted", lwd = 2)
title("Air Passenger Numbers")

When analysing air passenger data for the time series in question, we can see that up until 2020, there has been a predictable seasonal fluctuation in passenger numbers. When COVID-19 arrived in 2020 — this was followed by a sharp drop in passenger numbers followed by a swift uptrend in the same as travel restrictions started to lessen.

Using a 50% to 90% probability range, a forecast for the next 12 time periods can be generated:

# 50% to 90% probability intervals
plot(forecast(flights_structTS, level = c(50, 90), h = 12), xlim = c(2020, 2023))

Here is the forecast from the local level structural model:

In addition to the above forecast, it is also possible to generate a Dynamic Linear Model using the dlm package in R for forecasting purposes.

Dynamic Linear Modelling

For context, a dynamic linear model is one where distributional properties of the time series such as mean and variance are allowed to change over time — thus allowing a forecast to account for sudden changes or “shocks” in a time series.

Using R, the dynamic linear model is built and standardized prediction errors are generated:

# Dynamic Linear Model
buildFlights <- function(theta) {dlmModPoly(order = 1, dV = theta[1], dW = theta[2])}

fit <- dlmMLE(flights_ts, parm = c(100, 2), buildFlights, lower = rep(1e-4, 2))
fit

modFlights <- buildFlights(fit$par)
drop(V(modFlights))
drop(W(modFlights))

smoothFlights <- dlmSmooth(flights_ts, modFlights)
smoothFlights

# Generate standardized prediction errors
filterFlights <- dlmFilter(flights_ts, modFlights)
plot(residuals(filterFlights, sd = FALSE), type = "o", ylab = "Standardized prediction error", xlab='Year')
abline(h = 0)
title("Standardized prediction errors")

Note that the dlmMLE function is being used to estimate the maximum likelihood estimator of the unknown parameters, while the dlmSmooth function calculates smoothed values of the state vectors along with their variance/covariance matrices. dlmFilter computes the filtered values of the state vectors along with their variance/covariance matrices.

Before generating the overall forecast, let us firstly look at the standardized prediction errors that were generated:

When looking at the above graph, we can see that the standardized prediction errors were greater in magnitude near the beginning of 2020 — when passenger traffic dropped to historically low levels as a result of the pandemic. The purpose of incorporating these prediction errors into the eventual forecast is to allow the model to generate a probability forecast of potential values given forecast errors observed in the past.

Model Forecast

Using the dlmForecast function, the expected value of future observations and system states is generated. This particular forecast is generating forecasts for 12 steps ahead:

# DLM Forecast
foreFlights <- dlmForecast(filterFlights, nAhead = 12)
attach(foreFlights)


# Probability Bounds
hwidth <- qnorm(0.25, lower = FALSE) * sqrt(unlist(Q))
fore <- cbind(f, as.vector(f) + hwidth %o% c(-1, 1))
rg <- range(c(fore, window(flights_ts, start = c(2005, 7))))

Note that the fore vector above is generating a mean forecast as well as upper and lower bounds for the forecast of air passenger numbers.

Here are the results generated:

Now, the forecasts can be plotted, as well as the observed and smoothed levels:

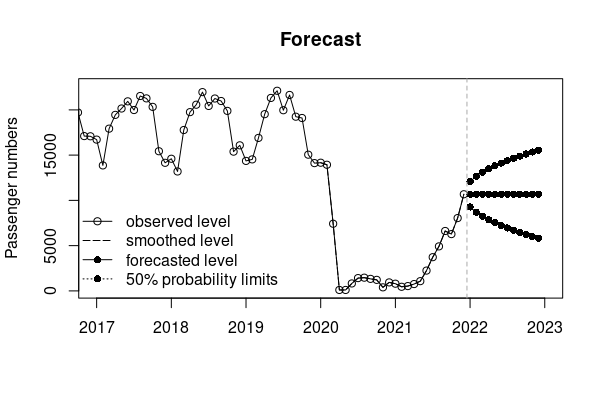
From this, we can see that a mean value of 10,678 passengers per month are predicted, with a lower bound of 5,806 and an upper bound of 15,549.

> flights_ts_2 <- ts(mydata$passenger_count[199:210], start = c(2022,1), frequency = 12)
> flights_ts_2
       Jan   Feb   Mar   Apr   May   Jun   Jul   Aug   Sep   Oct   Nov   Dec
2022  7304  6140 11193 14017 18235 19186 16608 16931 17402 17314 15710 17163
> 
> plot(flights_ts_2, type = "o", ylab='Passenger Numbers', xlab='Year') 
> title("Passenger Numbers for the year 2022")
> summary(flights_ts_2)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   6140   13311   16770   14767   17336   19186

When looking at the actual passenger numbers for 2022, we can see that the mean value came in at 14,767 while the minimum recorded was 6,140 and the maximum recorded was 19,186.

From this standpoint, the generated forecasts were more on the conservative side. However, the mean was still within the range as generated by the predictive model, and lower than the maximum value of 15,549.

In this regard, the forecast generated by the dynamic linear model allowed for a prediction of the range where we can expect the mean passenger numbers to lie. The advantage of the dynamic linear model is its ability to adapt quickly to new data, and as such the model was able to take into account the swift recovery in passenger numbers following the initial pandemic slump.

Conclusion

In this article, you have seen:

How to use StructTS to generate a Structural Time Series Model
How to interpret probability forecasts of a local level structural model
Use of dynamic linear models and generation of standardized prediction errors
Forecast techniques using dynamic linear models

Many thanks for your time, and please let me know if you have any questions or feedback.