Multilevel modelling with lme4: Analysing e-commerce sales
Published Jul 12, 2024 by Michael Grogan
Multilevel modelling allows for analysis of data that have hierarchical or clustered structures.
This is particularly useful in the context of market research, whereby segmenting customers by category (e.g. demographics, purchasing habits) is important in understanding how a business can both attract new customers and improve customer loyalty among existing ones.
The lme4 library in R is used to create multilevel models. One significant example of a multilevel modelling exercise within this library is that of the sleepstudy example, whereby a multilevel model was used to analyse how reaction times across sleep deprived individuals differed between participants given the number of days of sleep deprivation.
How would we apply such a model to analysing customer data? Let’s take a look!
Context
An e-commerce site wishes to analyse some recent sales data that they have collected regarding activity on their site. Specifically, they wish to determine factors that influence spend per customer.
They provide a dataset containing the following information:
Spend
Minutes on site
Category of product purchased
They wish to not only determine whether the number of minutes on site influences spending patterns, but also whether this differs depending on the category of product purchased by the customer.
Let us see how multilevel modelling can allow us to answer this.
Learn More
Are you interested in learning more about the power of Python and R in the market research space?
Overview
Here is an overview of the dataset we will work with.
> head(mydata,10)
spend minutes category
1 40 1 Clothing
2 117 2 Furniture
3 851 3 Technology
4 88 4 Home Appliances
5 10 5 Clothing
6 286 6 Furniture
7 446 7 Technology
8 79 8 Home AppliancesThe dataset contains 100 observations, detailing the amount spent by a customer in dollars, the number of minutes spent on the site before making a purchase, and the category of product purchased.
25 observations across four product categories are included in the dataset - namely Clothing, Furniture, Home Appliances, and Technology.
Let us generate a plot of spend versus minutes on the site:
ggplot(mydata, aes(minutes, spend, group=category, colour=category)) +
geom_point() +
facet_wrap(~category, ncol=9) +
scale_x_continuous(limits=c(0, 10),breaks=c(0,10)) +
theme_minimal()The below graphs plot spend versus minutes on site for each of the four product categories in the dataset.

We can see that the degree of spend across the four product categories differs significantly, with customers spending significantly more on technology than clothing products, for instance.
Model Building
Let us firstly run a simple linear regression whereby all customers are modeled solely on spend, with no relation between spend and minutes on site.
Model 1
> model1<-lm(spend ~ 1)
> summary(model1)
Call:
lm(formula = spend ~ 1)
Residuals:
Min 1Q Median 3Q Max
-203.37 -142.62 -66.87 91.38 637.63
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 213.37 19.05 11.2 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 190.5 on 99 degrees of freedomNow, let us plot the generated regression lines.
datafit=fitted(model1)
ggplot(mydata, aes(minutes, spend, group=category, colour=category)) +
geom_point() +
geom_line(aes(y=datafit), linetype=2) +
facet_wrap(~category, ncol=9) +
scale_x_continuous(limits=c(0, 10),breaks=c(0,10)) +
theme_minimal()We can see that the regression lines across all the plots are flat - which we would expect as minutes on site has not been included as an independent variable.

Now, let us adjust for categories, i.e. create a model whereby spend differs by product category but we are not considering minutes on site as a variable.
Model 2
> model2 <- lmer(spend ~ 1 + (1|category),mydata)
> summary(model2)
Linear mixed model fit by REML ['lmerMod']
Formula: spend ~ 1 + (1 | category)
Data: mydata
REML criterion at convergence: 1262.4
Scaled residuals:
Min 1Q Median 3Q Max
-2.5094 -0.4251 -0.0761 0.3358 3.3707
Random effects:
Groups Name Variance Std.Dev.
category (Intercept) 25114 158.5
Residual 17282 131.5
Number of obs: 100, groups: category, 4
Fixed effects:
Estimate Std. Error t value
(Intercept) 213.37 80.32 2.657In this case, the model is acknowledging that product spend differs by category, and adjusts for this accordingly by generating fixed and random effects.
However, minutes on site is not considered as an independent variable.
The generated plots are as follows:

We see that the fit of the regression lines are adjusted to account for the fact that spend differs across product categories, but minutes on site have not been considered as an independent variable.
Model 3
Now, let us consider a model whereby the number of minutes on site is included as a variable - but it is assumed that minutes on site does not differ between categories - i.e. the influence of minutes on site on customer spend is assumed to be the indpendent of product category.
> model3 <- lmer(spend ~ 1 + minutes + (1|category),mydata)
> summary(model3)
Linear mixed model fit by REML ['lmerMod']
Formula: spend ~ 1 + minutes + (1 | category)
Data: mydata
REML criterion at convergence: 1259.1
Scaled residuals:
Min 1Q Median 3Q Max
-2.5473 -0.4052 -0.0638 0.3435 3.4265
Random effects:
Groups Name Variance Std.Dev.
category (Intercept) 25108 158.5
Residual 17419 132.0
Number of obs: 100, groups: category, 4
Fixed effects:
Estimate Std. Error t value
(Intercept) 201.5750 83.7698 2.406
minutes 0.9073 1.8302 0.496
Correlation of Fixed Effects:
(Intr)
minutes -0.284The generated plots are as follows:

Model 4
Finally, let us adjust the model to both include the number of minutes on site as a variable, but allow this variable to differ across product categories.
In other words, we want the multilevel model to recognize that while customer spend may differ depending on the minutes spent on site - this could also depend on the product category in question, i.e. a customer purchasing technology products may need less time to make their choice of product than a customer purchasing furniture products, for instance.
> model4 <- lmer(spend ~ 1 + minutes + (1 + minutes|category),mydata)
> summary(model4)
Linear mixed model fit by REML ['lmerMod']
Formula: spend ~ 1 + minutes + (1 + minutes | category)
Data: mydata
REML criterion at convergence: 1253.8
Scaled residuals:
Min 1Q Median 3Q Max
-2.4983 -0.4456 -0.0236 0.4242 3.0670
Random effects:
Groups Name Variance Std.Dev. Corr
category (Intercept) 41159.18 202.877
minutes 39.63 6.295 -0.68
Residual 15792.04 125.666
Number of obs: 100, groups: category, 4
Fixed effects:
Estimate Std. Error t value
(Intercept) 201.5750 104.6946 1.925
minutes 0.9073 3.5978 0.252
Correlation of Fixed Effects:
(Intr)
minutes -0.684
> fixef(model4)
(Intercept) minutes
201.5750000 0.9073077
> ranef(model4)
$category
(Intercept) minutes
Clothing -181.39908 1.338642
Furniture -40.48363 6.715551
Home Appliances -59.00663 -1.518628
Technology 280.88933 -6.535565
with conditional variances for “category” When analysing the above results, it is notable that we see different spending patterns based on the number of minutes each customer spends on the site. Here is a plot of the results.
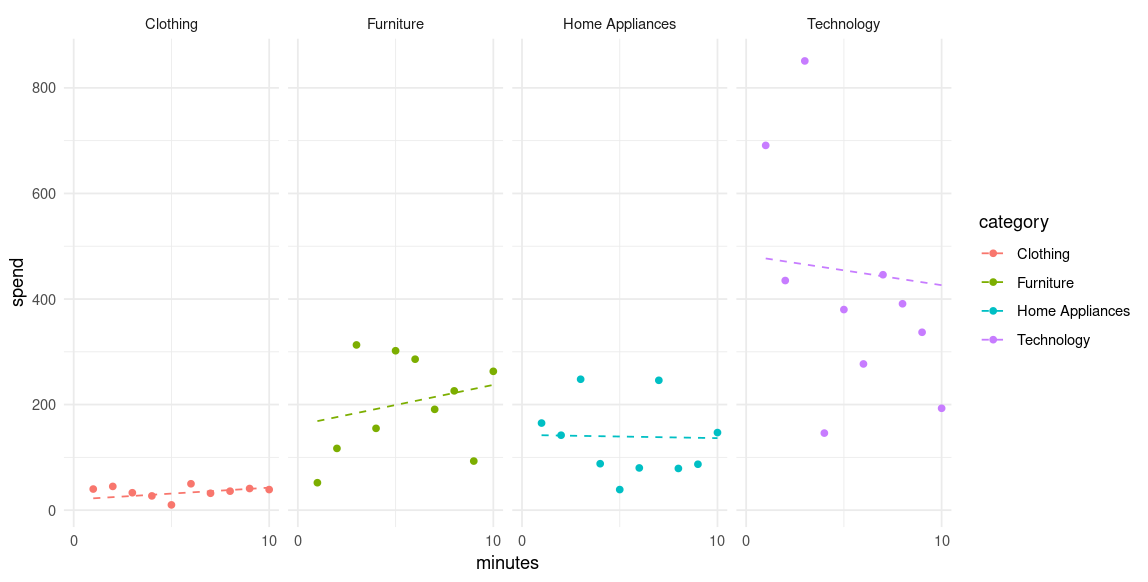
For instance, we see that there is a positive relationship between spend and time on site for furniture products, but a negative one for technology products.
Why might this be? It could be the case that a technology customer considering an expensive purchase has already researched their options in detail, and thus those customers spending more time on the site are less sure of their buying intention.
In contrast, a customer in the market for furniture products may be taking the time to consider what is available on the site — and thus those who spend longer on the site may be more inclined to spend more.
Here is a calculation of the random slopes:
> rand_slopes <- ranef(model4)$category$minutes + fixef(model4)["minutes"]
> rand_slopes
[1] 2.2459500 7.6228589 -0.6113206 -5.6282575We see that the slope of 7.62 for Furniture indicates that each additional minute spent on site increases dollar spend by 7.62, while a slope of -5.62 for Technology means that there is a decrease in dollar spend of -5.62 for each additional minute spent on site.
Conclusion
In this article, you have seen how multilevel modelling can be used for customer segment analysis. Specifically, we have used multilevel modelling to segment customers by product category, and analyse how spend is impacted by minutes on site with respect to each category.