Forecasting Air Passenger Volatility Using GARCH Modelling

Published Jun 17, 2023 by Michael Grogan

When attempting to forecast a time series, consideration is given as to both the trend and seasonality patterns in the series.

That said, we can often come across a time series where the volatility in the series is not constant over time. This is known as autoregressive conditional heteroscedasticity.

In this regard, a GARCH model can be used to forecast the volatility in a time series. The purpose of this article is to illustrate how to test for the presence of autoregressive conditional heteroscedasticity using air passenger data sourced from DataSF Open Data and then build a GARCH model to forecast volatility for this time series.

Learn More

Are you interested in learning more about how to forecast business data using time series analysis?

Book a free 30 minute consultation with me on Calendly.

Time series with no ARCH present

To illustrate this better, let us consider a series of normally distributed random numbers in R — formatted as a yearly time series.

df<-rnorm(100)
tsrnorm <- ts(df, start = c(2015,3), frequency = 12)
plot(tsrnorm,type="l",ylab="Values")
title("Values")

Plotting this time series yields the following:

Source: Plot generated in R using the Air Traffic Passenger Statistics dataset from DataSF Open Data.

Using the ARCH test for univariate time series from the MTS library in R, we can see that the null hypothesis of no presence of conditional heteroscedasticity cannot be rejected at the 5% level of significance, with p-values significantly above 0.05.

> archTest(tsrnorm)
Q(m) of squared series(LM test):  
Test statistic:  10.51308  p-value:  0.3966882 
Rank-based Test:  
Test statistic:  13.04079  p-value:  0.2213999

When generating an ARIMA forecast on this series using auto.arima, we can see that an ARIMA(0,0,0) model is selected as the model of best fit — which is in line with what we expect given that the time series generated is essentially white noise.

> fitarima<-auto.arima(tsrnorm, trace=TRUE, test="kpss", ic="bic")

 ARIMA(2,0,2)(1,0,1)[12] with non-zero mean : 305.4602
 ARIMA(0,0,0)            with non-zero mean : 283.2293
 ARIMA(1,0,0)(1,0,0)[12] with non-zero mean : 288.6238
 ARIMA(0,0,1)(0,0,1)[12] with non-zero mean : 288.5743
 ARIMA(0,0,0)            with zero mean     : 278.7719
 ARIMA(0,0,0)(1,0,0)[12] with non-zero mean : 285.6014
 ARIMA(0,0,0)(0,0,1)[12] with non-zero mean : 285.7997
 ARIMA(0,0,0)(1,0,1)[12] with non-zero mean : 290.1935
 ARIMA(1,0,0)            with non-zero mean : 285.7561
 ARIMA(0,0,1)            with non-zero mean : 285.4466
 ARIMA(1,0,1)            with non-zero mean : 289.4372

 Best model: ARIMA(0,0,0)            with zero mean

When plotting the residuals of the ARIMA model, we can see that the variance looks to be constant.

> plot(residuals(fitarima))
> title("Residuals of ARIMA Model")

Now, let us analyse a time series where ARCH is present — specifically air passenger numbers from DataSF Open Data.

Time series with ARCH present

The dataset used for this example is the Air Traffic Passenger Statistics dataset from DataSF Open Data, which is licensed under the Public Domain and Dedication License (PDDL). It was chosen to analyse historical air passenger data for British Airways — specifically for enplaned passengers travelling internationally to Europe from July 2005 to December 2022.

When running archTest once again, we can see that with a p-value of 0, the null hypothesis of no autoregressive conditional heteroscedasticity is rejected at the 5% level, indicating that ARCH effects are present in the time series.

> archTest(flights_ts)
Q(m) of squared series(LM test):  
Test statistic:  559.1083  p-value:  0 
Rank-based Test:  
Test statistic:  315.6464  p-value:  0

Let us fit an ARIMA model to the data and plot the residuals:

> # ARIMA
> fitarima<-auto.arima(flights_ts, trace=TRUE, test="kpss", ic="bic")

 Fitting models using approximations to speed things up...

 ARIMA(2,0,2)(1,1,1)[12] with drift         : 3335.057
 ARIMA(0,0,0)(0,1,0)[12] with drift         : 3768.406
 ARIMA(1,0,0)(1,1,0)[12] with drift         : 3363.064
 ARIMA(0,0,1)(0,1,1)[12] with drift         : 3553.438
 ARIMA(0,0,0)(0,1,0)[12]                    : 3763.431
 ARIMA(2,0,2)(0,1,1)[12] with drift         : 3321.197
 ARIMA(2,0,2)(0,1,0)[12] with drift         : 3389.068
 ARIMA(2,0,2)(0,1,2)[12] with drift         : 3325.333
 ARIMA(2,0,2)(1,1,0)[12] with drift         : 3369.368
 ARIMA(2,0,2)(1,1,2)[12] with drift         : 3333.489
 ARIMA(1,0,2)(0,1,1)[12] with drift         : 3313.035
 ARIMA(1,0,2)(0,1,0)[12] with drift         : 3383.34
 ARIMA(1,0,2)(1,1,1)[12] with drift         : 3339.011
 ARIMA(1,0,2)(0,1,2)[12] with drift         : 3317.092
 ARIMA(1,0,2)(1,1,0)[12] with drift         : 3365.819
 ARIMA(1,0,2)(1,1,2)[12] with drift         : 3333.249
 ARIMA(0,0,2)(0,1,1)[12] with drift         : 3452.153
 ARIMA(1,0,1)(0,1,1)[12] with drift         : 3307.936
 ARIMA(1,0,1)(0,1,0)[12] with drift         : 3379.521
 ARIMA(1,0,1)(1,1,1)[12] with drift         : 3334.918
 ARIMA(1,0,1)(0,1,2)[12] with drift         : 3312.17
 ARIMA(1,0,1)(1,1,0)[12] with drift         : 3360.67
 ARIMA(1,0,1)(1,1,2)[12] with drift         : 3328.116
 ARIMA(1,0,0)(0,1,1)[12] with drift         : 3305.58
 ARIMA(1,0,0)(0,1,0)[12] with drift         : 3378.07
 ARIMA(1,0,0)(1,1,1)[12] with drift         : 3332.445
 ARIMA(1,0,0)(0,1,2)[12] with drift         : 3309.485
 ARIMA(1,0,0)(1,1,2)[12] with drift         : 3325.783
 ARIMA(0,0,0)(0,1,1)[12] with drift         : Inf
 ARIMA(2,0,0)(0,1,1)[12] with drift         : 3310.926
 ARIMA(2,0,1)(0,1,1)[12] with drift         : 3316.098
 ARIMA(1,0,0)(0,1,1)[12]                    : 3300.346
 ARIMA(1,0,0)(0,1,0)[12]                    : 3372.808
 ARIMA(1,0,0)(1,1,1)[12]                    : 3327.214
 ARIMA(1,0,0)(0,1,2)[12]                    : 3304.261
 ARIMA(1,0,0)(1,1,0)[12]                    : 3357.83
 ARIMA(1,0,0)(1,1,2)[12]                    : 3320.579
 ARIMA(0,0,0)(0,1,1)[12]                    : 3749.671
 ARIMA(2,0,0)(0,1,1)[12]                    : 3305.756
 ARIMA(1,0,1)(0,1,1)[12]                    : 3302.772
 ARIMA(0,0,1)(0,1,1)[12]                    : 3558.329
 ARIMA(2,0,1)(0,1,1)[12]                    : 3310.924

 Now re-fitting the best model(s) without approximations...

 ARIMA(1,0,0)(0,1,1)[12]                    : 3512.789

 Best model: ARIMA(1,0,0)(0,1,1)[12]

The model of best fit is determined as ARIMA(1,0,0)(0,1,1)[12].

Here is a plot of the residuals:

When looking at the above — we can see that the residuals showed the most volatility during 2020 when air passenger traffic fell dramatically due to COVID-19, along with increased volatility in 2010 following the financial crisis.

As such, we can see that the variance in the time series is clearly not constant over time. The series seems to have periods of relatively low variance followed by periods of high variance.

In this regard, let us use GARCH to model this volatility.

GARCH Forecast

Firstly, let us specify the GARCH model using the rugarch library in R.

> # start with default GARCH spec.
> library(rugarch)
> spec = ugarchspec() #the empty function specifies the default model. 
> print(spec)

*---------------------------------*
*       GARCH Model Spec          *
*---------------------------------*

Conditional Variance Dynamics  
------------------------------------
GARCH Model  : sGARCH(1,1)
Variance Targeting : FALSE 

Conditional Mean Dynamics
------------------------------------
Mean Model  : ARFIMA(1,0,1)
Include Mean  : TRUE 
GARCH-in-Mean  : FALSE 

Conditional Distribution
------------------------------------
Distribution :  norm 
Includes Skew :  FALSE 
Includes Shape :  FALSE 
Includes Lambda :  FALSE#

Now, a volatility forecast can be conducted for 10 steps ahead:

> fit = ugarchfit(data = flights_ts, spec = spec, out.sample=10)
> forc1 = ugarchforecast(fit, n.ahead=10, n.roll = 10)
> forc1

*------------------------------------*
*       GARCH Model Forecast         *
*------------------------------------*
Model: sGARCH
Horizon: 10
Roll Steps: 10
Out of Sample: 10

0-roll forecast [T0=Feb 2022]:
     Series Sigma
T+1    6876  1964
T+2    7680  1964
T+3    8428  1964
T+4    9124  1963
T+5    9772  1963
T+6   10374  1963
T+7   10934  1963
T+8   11456  1963
T+9   11941  1963
T+10  12392  1963

Here is a plot of the forecasts:

We can see that the forecast series with unconditional 1-Sigma bands trends upwards — demonstrating a rebound in air passenger numbers following the COVID-19 pandemic. It should be noted that the forecasting model only seeks to forecast using the signal and not the noise from the specified time series. As such, we can expect that the forecast will be significantly less volatile than that of the time series itself.

For instance, let us lengthen the forecast to 100 steps ahead, and see what the forecast generates:

library(rugarch)
spec = ugarchspec() #the empty function specifies the default model. 
print(spec)
fit = ugarchfit(data = flights_ts, spec = spec, out.sample=10)
forc1 = ugarchforecast(fit, n.ahead=100, n.roll = 10)
forc1
plot(forc1, which = "all")

We can see that passenger numbers eventually smooth out, and ultimately oscillate within the range seen before the pandemic:

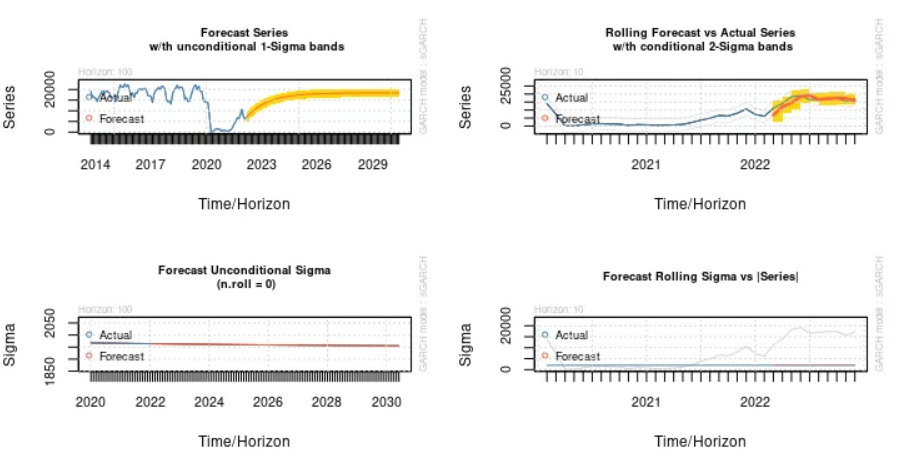
Of course, while we can expect that there could be significant deviations from the forecasted range over the forecasted period — the GARCH forecast is focusing on the overall signal rather than random noise in the series.

In this regard, we can see that GARCH is a useful tool for forecasting volatility in a situation where a simple ARIMA forecast would likely fall short due to the inability of the model to forecast periods of randomly high volatility.

Conclusion

In this article, we have seen:

How to test for ARCH effects using R
Plot and analyse ARIMA model residuals
Conduct a volatility forecast using GARCH

Many thanks for your time, and please let me know if you have any questions or feedback.

Are you interested in learning more about how to forecast business data using time series analysis? Book a free 30 minute consultation with me on Calendly.

Learn More

Time series with no ARCH present

Time series with ARCH present

GARCH Forecast

Conclusion

References